Greedy Algorithm
- optimization problem을 풀 때 사용
- dynamic programming이 너무 과도할 때(복잡할 때) greedy로 더 쉽게 풀 수 있다.
- 현재 상황에서 최선의 답을 선택. 현재 상황의 최선이 전체의 최선이길 바라면서 푼다.
- Greedy choice property(앞의 선택이 이후의 선택에 영향을 주지 않는 조건)를 만족할 때 사용한다.
- 현재 상황에서는 최선이지만 전체에서 최선이라는 보장은 없다.
- greedy로 풀 수 있는 문제는 모두 dynamic programming으로 풀 수 있다.
- top-down 구조 (dynamic은 bottom up)
- ex) 가방채우기 문제, 허프만 코드, 크루스컬 MST, 프림 MST, SSSP
Counting money
6.39$를 만든다고 하자.
- $5 bill
- $1 bill, to make $6
- 25¢ coin, to make $6.25
- 10¢ coin, to make $6.35
- four 1¢ coins, to make $6.39
US 달러에 대해서는 greedy algorithm으로 optimum solution을 풀 수 있다.
그런데 만약 krons라는 화폐가 있다면? (a faliure of the greedy algorithm)
이 화폐는 1kron, 7kron, 10kron의 동전으로 이루어져있다.
그리디 알고리즘으로 15krons를 만든다면
- 10 kron bill, to make 10kron
- five 1kron, to make 15kron
총 6개의 동전이 필요하다.
하지만 7kron 2개, 1kron 1개를 내면 3개의 동전으로 더 적다. 이렇게 그리디 알고리즘은 모든 케이스에 맞는 답을 내지는 않는다.
즉, 이 경우에 Greedy Algorithm은 답을 냈지만 최적해는 아니다.
Activity-selection Problem(활동 선택 문제)
여러개의 activity가 있을 때, 각 activity의 시작시간, 종료시간을 보고 최대 몇개의 활동을 할 수 있을까?
Input : activity 집합의 시작시간: Si, 종료 시간Fi
Output : 최대 할 수 있는 활동의 집합
예시)
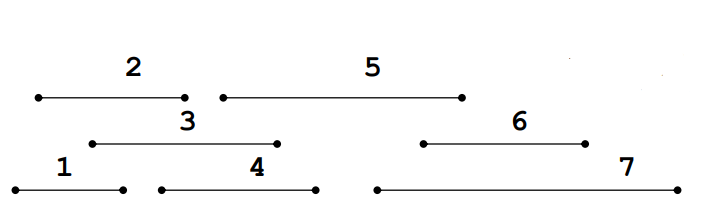
그림의 경우 {1, 4, 7}의 활동이 한번에 가능하다.
만약 이걸 Dynamic Programming으로 푼다면?
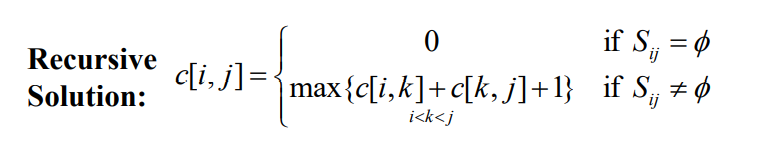
복잡하다.
-> Greedy로 훨씬 간단하게 풀 수 있다.
- 종료시간은 오름차순 정렬
- 첫번째 활동을 넣고 시작
- 이전 활동이 끝나는 시간 이후에 시작하는 activity를 넣는다.
- 더이상의 활동이 없을 때 까지 반복한다.
증명
현재 상황에서 선택할수 있는 가장 빠른 활동을 선택하지 않는 경우가 있다해도, 그것은 빠른 활동을 선택한 경우로 대체가 가능하다.
Greedy Algorithms vs. Dynamic Programming
- 표에서 볼 수 있듯 Greedy로 풀 수 있는 문제는 무조건 DP로 풀 수 있지만(DP가 더 Powerfull 하다. ) DP를 무조건 Greedy로 풀 수 있지는 않다.
- 그리디와 DP 모두 Optimization 문제를 풀 때 사용한다.
- DP는 하위 문제에 의존하지만 Greedy는 순간의 최선의 선택을 하며 이 선택은 하위문제에 의존하지 않는다.
- greedy를 언제 써야 하는지 알아차리기 어렵다. -> DP로 먼저 풀어보고 선택을 이해한 후 눈앞의 선택이 다른 선택보다 나은지 확인한 후 문제를 푼다.
The Knapsack Problem(가방 채우기 문제)
- 가방에 담을 수 있는 무게가 정해져있을 때, 가방에 담은 물건들의 가치가 최고가 되도록 선택하는 문제
- 가방 최대 용량 W
- set S는 n개의 물건으로 구성
- wi : 아이템 i의 무게
- bi : 아이템 i의 가치
방법1. 0-1 knapsack problem
- item을 넣거나 안넣거나

- brute-force approach로 푼다면?
-> O(2^n)
- Dynamic problem으로 푼다면?
Sk={items labeled 1,2,...,k}
물건을 빼고 다른걸 넣을 수 있기 때문에 Sn이 Sk의 부분의 일부분이 아닐 수 있다. -> 오류!! 다시 생각해야한다.
-> 2차원 배열로 정의한다.
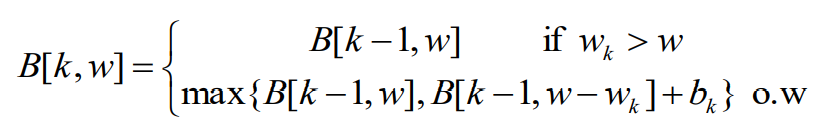
case1 : wk>w이면 item k는 너무 무거워서 배낭에 넣을 수 없다.
ex) 처음에 배낭이 20kg이고 w1=2kg이므로 배낭에 넣을 수 있다. item1을 넣는다는 선택을 하면 최대 가격은 3+18kg에 넣을 수 있는 최대 가격이 된다. 즉, 18kg에 남은 물건을 넣는 부분 문제가 된다.
case2 : wk≤w이면 item k를 넣지 않았을때와 넣었을때의 가격중 최대를 택한다.
ex) 만약 item1을 넣지 않는 선택을 하면 최대가격은 0+20kg에 남은 물건을 넣을 수 있는 최대 가격이 된다. 즉, 20kg에 남은 물건을 넣는 부분문제가 된다.
Running time : O(n*W)
- Greedy로는 풀 수 없다.
방법2. fracional knapsack problem (아이템을 잘라서 가져갈 수 있다.)
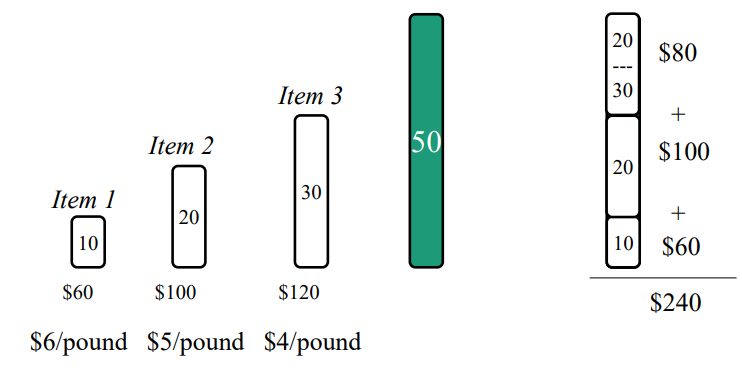
- Greedy로 풀 수 있다.
각각의 단위 무게당 값어치를 따진 후 높은것부터 집어넣는다.
Runnung tima : item이 정렬되어있을 경우 : O(n), 아니면 O(nlogn)
Huffman Code Problem
- 한글이 포함된 문자는 16bit유니코드를 사용한다. 영어만 포함된 문자는 8bit ASCII코드를 사용한다. 영어로 1,000자를 작성했다면 8 X 1,000 bit 를 차지하게 된다.
- 이 파일 크기를 줄이기 위해 허프만코드를 이용해 데이터를 압축한다.
- 빈도수가 많은 문자에 적은 비트를 할당하여 데이터를 압축하는 방식이다.
- 허프만 코드는 prefix 코드인다.
* prefix-free : 어떤 코드도 다른 코드의 접두사로 나오지 않는다. -> decoding과정이 명확해진다.
20%~90%로 사이즈를 줄일 수 있다.
- 단어 출현 빈도가 균일하면 허프만 코드(Variable-length codeword)는 ASCII(fixed-length codeword)에비해 이점이 없다.
- 허프만 압축 알고리즘 과정
- 발생 빈도수가 가장 낮은 두 문자를 선택해서 하나로 합친다.
- 왼쪽은 빈도수가 낮고 오른쪽은 높다.
- 빈도수가 같은 것 중에서는 작은 집합을 우선적으로 연결한다.
- 트리가 생성되면 차례대로 0,1 값을 부여한다. (왼쪽 0, 오른쪽 1)
예를 들어 a: 45, b: 13, c:12, d: 16, e: 9, f: 5 라면
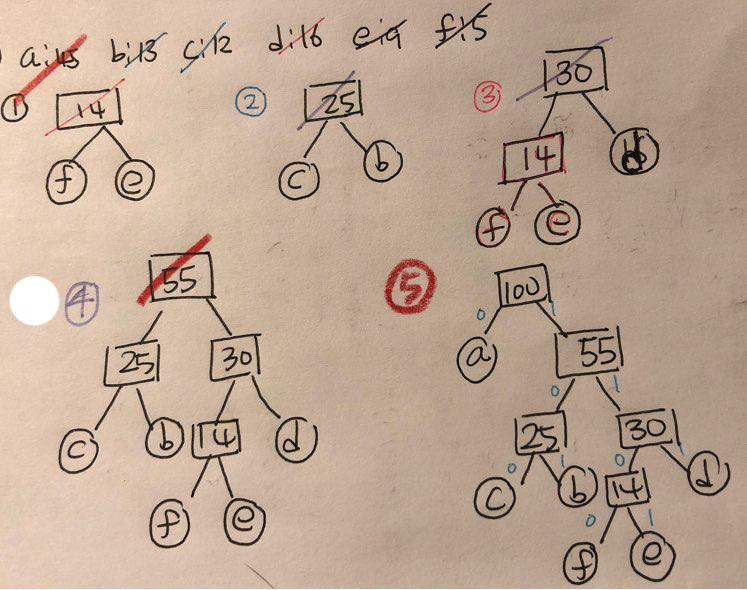
그림처럼 트리로 나타낸 후 해당 문자까지 타고 내려간다.
a: 0, c: 100, b: 101, d: 111, f: 1100, e: 1101
그렇다면 압축률은?
허프만 사용 : 45*1bit + (13+12+16)*3bit + (9+5)*4bit = 224bit
원래는 100개의 문자가 있었기 때문에 8bit X 100 = 800bit 였다.
즉 224/8000 = 28%로 원래의 28%로 압축되었다.
- Running time : O(nlogn)
- mp3, jpg format에 사용된다.
| Divide & Conquer | Dynamic Programming | Greedy Algorithm | |
| 하위 문제 | O | O | O |
| recursive | O | O | O |
| 하위 문제의 독립성 | O | X 연관이 있다. | O |
| 하위 문제의 갯수 | 어떻게 쪼개는지에 따라 달라짐 | typically small | 순서에 의존 |
| 전처리 할 때Runnung time | typically logn | 하위 문제의 수와 난이도에 달렸다. | nlogn 정렬 주로 사용 |
| 주로 optimization문제를 푼다. | O | O | |
| optimal substructure | O | O | |
| Greedy choice property | O | ||
| Heuristic, 경험적인 법칙에 이용 | O |
'💚알고리즘' 카테고리의 다른 글
| Shortest Path Problem(최단거리 문제) (0) | 2023.01.25 |
|---|---|
| Minimum SpanningTree(최소 비용 신장 트리) (1) | 2023.01.25 |
| Dynamic Programming (동적 계획법) (0) | 2023.01.25 |
| Binary Search Tree (이진 탐색 트리) (0) | 2023.01.25 |
| hash 알고리즘 (1) | 2023.01.25 |
Greedy Algorithm
- optimization problem을 풀 때 사용
- dynamic programming이 너무 과도할 때(복잡할 때) greedy로 더 쉽게 풀 수 있다.
- 현재 상황에서 최선의 답을 선택. 현재 상황의 최선이 전체의 최선이길 바라면서 푼다.
- Greedy choice property(앞의 선택이 이후의 선택에 영향을 주지 않는 조건)를 만족할 때 사용한다.
- 현재 상황에서는 최선이지만 전체에서 최선이라는 보장은 없다.
- greedy로 풀 수 있는 문제는 모두 dynamic programming으로 풀 수 있다.
- top-down 구조 (dynamic은 bottom up)
- ex) 가방채우기 문제, 허프만 코드, 크루스컬 MST, 프림 MST, SSSP
Counting money
6.39$를 만든다고 하자.
- $5 bill
- $1 bill, to make $6
- 25¢ coin, to make $6.25
- 10¢ coin, to make $6.35
- four 1¢ coins, to make $6.39
US 달러에 대해서는 greedy algorithm으로 optimum solution을 풀 수 있다.
그런데 만약 krons라는 화폐가 있다면? (a faliure of the greedy algorithm)
이 화폐는 1kron, 7kron, 10kron의 동전으로 이루어져있다.
그리디 알고리즘으로 15krons를 만든다면
- 10 kron bill, to make 10kron
- five 1kron, to make 15kron
총 6개의 동전이 필요하다.
하지만 7kron 2개, 1kron 1개를 내면 3개의 동전으로 더 적다. 이렇게 그리디 알고리즘은 모든 케이스에 맞는 답을 내지는 않는다.
즉, 이 경우에 Greedy Algorithm은 답을 냈지만 최적해는 아니다.
Activity-selection Problem(활동 선택 문제)
여러개의 activity가 있을 때, 각 activity의 시작시간, 종료시간을 보고 최대 몇개의 활동을 할 수 있을까?
Input : activity 집합의 시작시간: Si, 종료 시간Fi
Output : 최대 할 수 있는 활동의 집합
예시)

그림의 경우 {1, 4, 7}의 활동이 한번에 가능하다.
만약 이걸 Dynamic Programming으로 푼다면?
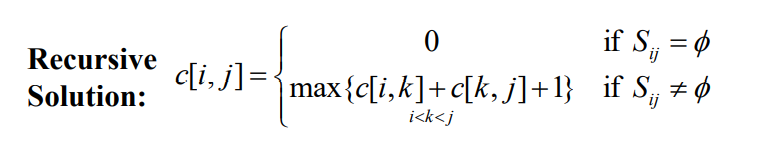
복잡하다.
-> Greedy로 훨씬 간단하게 풀 수 있다.
- 종료시간은 오름차순 정렬
- 첫번째 활동을 넣고 시작
- 이전 활동이 끝나는 시간 이후에 시작하는 activity를 넣는다.
- 더이상의 활동이 없을 때 까지 반복한다.
증명
현재 상황에서 선택할수 있는 가장 빠른 활동을 선택하지 않는 경우가 있다해도, 그것은 빠른 활동을 선택한 경우로 대체가 가능하다.
Greedy Algorithms vs. Dynamic Programming

- 표에서 볼 수 있듯 Greedy로 풀 수 있는 문제는 무조건 DP로 풀 수 있지만(DP가 더 Powerfull 하다. ) DP를 무조건 Greedy로 풀 수 있지는 않다.
- 그리디와 DP 모두 Optimization 문제를 풀 때 사용한다.
- DP는 하위 문제에 의존하지만 Greedy는 순간의 최선의 선택을 하며 이 선택은 하위문제에 의존하지 않는다.
- greedy를 언제 써야 하는지 알아차리기 어렵다. -> DP로 먼저 풀어보고 선택을 이해한 후 눈앞의 선택이 다른 선택보다 나은지 확인한 후 문제를 푼다.
The Knapsack Problem(가방 채우기 문제)
- 가방에 담을 수 있는 무게가 정해져있을 때, 가방에 담은 물건들의 가치가 최고가 되도록 선택하는 문제
- 가방 최대 용량 W
- set S는 n개의 물건으로 구성
- wi : 아이템 i의 무게
- bi : 아이템 i의 가치
방법1. 0-1 knapsack problem
- item을 넣거나 안넣거나

- brute-force approach로 푼다면?
-> O(2^n)
- Dynamic problem으로 푼다면?
Sk={items labeled 1,2,...,k}
물건을 빼고 다른걸 넣을 수 있기 때문에 Sn이 Sk의 부분의 일부분이 아닐 수 있다. -> 오류!! 다시 생각해야한다.
-> 2차원 배열로 정의한다.
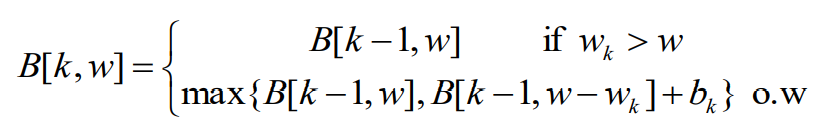
case1 : wk>w이면 item k는 너무 무거워서 배낭에 넣을 수 없다.
ex) 처음에 배낭이 20kg이고 w1=2kg이므로 배낭에 넣을 수 있다. item1을 넣는다는 선택을 하면 최대 가격은 3+18kg에 넣을 수 있는 최대 가격이 된다. 즉, 18kg에 남은 물건을 넣는 부분 문제가 된다.
case2 : wk≤w이면 item k를 넣지 않았을때와 넣었을때의 가격중 최대를 택한다.
ex) 만약 item1을 넣지 않는 선택을 하면 최대가격은 0+20kg에 남은 물건을 넣을 수 있는 최대 가격이 된다. 즉, 20kg에 남은 물건을 넣는 부분문제가 된다.
Running time : O(n*W)
- Greedy로는 풀 수 없다.
방법2. fracional knapsack problem (아이템을 잘라서 가져갈 수 있다.)

- Greedy로 풀 수 있다.
각각의 단위 무게당 값어치를 따진 후 높은것부터 집어넣는다.
Runnung tima : item이 정렬되어있을 경우 : O(n), 아니면 O(nlogn)
Huffman Code Problem
- 한글이 포함된 문자는 16bit유니코드를 사용한다. 영어만 포함된 문자는 8bit ASCII코드를 사용한다. 영어로 1,000자를 작성했다면 8 X 1,000 bit 를 차지하게 된다.
- 이 파일 크기를 줄이기 위해 허프만코드를 이용해 데이터를 압축한다.
- 빈도수가 많은 문자에 적은 비트를 할당하여 데이터를 압축하는 방식이다.
- 허프만 코드는 prefix 코드인다.
* prefix-free : 어떤 코드도 다른 코드의 접두사로 나오지 않는다. -> decoding과정이 명확해진다.
20%~90%로 사이즈를 줄일 수 있다.
- 단어 출현 빈도가 균일하면 허프만 코드(Variable-length codeword)는 ASCII(fixed-length codeword)에비해 이점이 없다.
- 허프만 압축 알고리즘 과정
- 발생 빈도수가 가장 낮은 두 문자를 선택해서 하나로 합친다.
- 왼쪽은 빈도수가 낮고 오른쪽은 높다.
- 빈도수가 같은 것 중에서는 작은 집합을 우선적으로 연결한다.
- 트리가 생성되면 차례대로 0,1 값을 부여한다. (왼쪽 0, 오른쪽 1)
예를 들어 a: 45, b: 13, c:12, d: 16, e: 9, f: 5 라면

그림처럼 트리로 나타낸 후 해당 문자까지 타고 내려간다.
a: 0, c: 100, b: 101, d: 111, f: 1100, e: 1101
그렇다면 압축률은?
허프만 사용 : 45*1bit + (13+12+16)*3bit + (9+5)*4bit = 224bit
원래는 100개의 문자가 있었기 때문에 8bit X 100 = 800bit 였다.
즉 224/8000 = 28%로 원래의 28%로 압축되었다.
- Running time : O(nlogn)
- mp3, jpg format에 사용된다.
| Divide & Conquer | Dynamic Programming | Greedy Algorithm | |
| 하위 문제 | O | O | O |
| recursive | O | O | O |
| 하위 문제의 독립성 | O | X 연관이 있다. | O |
| 하위 문제의 갯수 | 어떻게 쪼개는지에 따라 달라짐 | typically small | 순서에 의존 |
| 전처리 할 때Runnung time | typically logn | 하위 문제의 수와 난이도에 달렸다. | nlogn 정렬 주로 사용 |
| 주로 optimization문제를 푼다. | O | O | |
| optimal substructure | O | O | |
| Greedy choice property | O | ||
| Heuristic, 경험적인 법칙에 이용 | O |
'💚알고리즘' 카테고리의 다른 글
| Shortest Path Problem(최단거리 문제) (0) | 2023.01.25 |
|---|---|
| Minimum SpanningTree(최소 비용 신장 트리) (1) | 2023.01.25 |
| Dynamic Programming (동적 계획법) (0) | 2023.01.25 |
| Binary Search Tree (이진 탐색 트리) (0) | 2023.01.25 |
| hash 알고리즘 (1) | 2023.01.25 |
